(1)
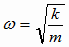 =
=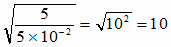 [rad/s]
[rad/s](2) v=Aω=0.10×10=1.0 [m/s] a=Aω2=0.10×102=10 [m/s2]
第18回 4月29日
前回(第17回)の練習問題の解答
1 問題よりA=0.15 ω=2π
(1)
v=Aω=0.15×2×π=0.3×3.14≒0.94 [m/s]
(2) a=Aω2=0.15×4π2=0,6×(3.14)2≒5.9
[m/s2]
F=-mω2x
mω2A=0.5×4π2×0.15≒3.0
[N]
2 m =5.0×10-2
k=5.0 A=0.10
(1)
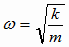 =
=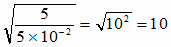 [rad/s]
[rad/s]
![]() =0.2×3.14≒0.63
[s]
=0.2×3.14≒0.63
[s]
(2) v=Aω=0.10×10=1.0 [m/s]
a=Aω2=0.10×102=10
[m/s2]
3 (1)つり合いの位置 l+a
(2)
a
(3)つり合いの位置で、mg=ka
これより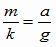 よって
よって ![]() =2π
=2π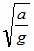
(4)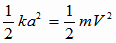 これより
これより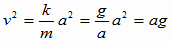 よって
よって 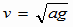
4 (1)
ばね振り子 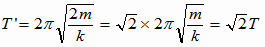
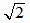 倍
倍
単振り子 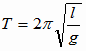 質量によらないので 1倍
質量によらないので 1倍
(2) ばね振り子 1倍
単振り子 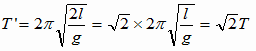
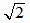 倍
倍
(3) ばね振り子 1倍
単振り子 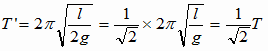
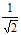 倍
倍
5 (1)
つりあいの位置からx変位すると-kxの復元力がはたらき、復元力の定数は水平ばね振り子と同じなので
![]()
(2)
つりあいの位置が中心なので、そのときの、斜面方向の力のつりあいを考える。
重力の斜面方向の分力の大きさはmgsinθ であり、それがばねによる弾性力とつりあうので、
kx=mgsinθ
これより x=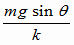
|
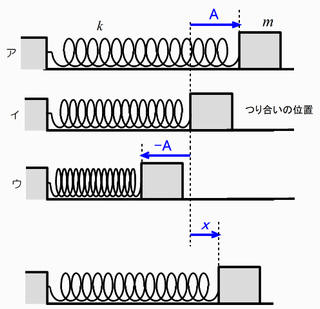
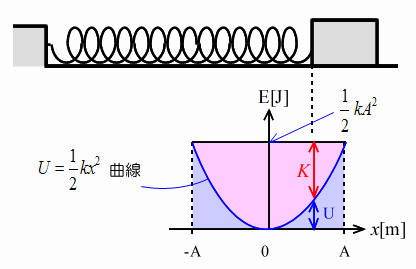
単振動とエネルギー 今回は単振動のエネルギーについて考えましょう。右図のように、なめらかな床に置いたの重り(質量m[kg])に左端を固定したばね(ばね定数k[N/m]をつけて、ばねが自然長になる位置から右にA[m]変位させた状態で手をはなすと、ア→イ→ウ→イ→ア→‥‥と続く振幅Aの単振動が起こります。 重りの速さが最も大きいのはア~ウのうちどれでしょうか? イの時ですね。振動中心通る時の速さが最大です。つまり重りの運動エネルギーが最大になる時です。そのときの重りの速さをVとすると、運動エネルギーは 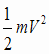 です。 です。この運動エネルギーはもともとアでばねに蓄えられた弾性力による位置エネルギーが変化したものです。アでばねに蓄えられた弾性力による位置エネルギーは 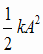 でした。 でした。さて、もし摩擦力などの非保存力がはたらかなければ、力学的エネルギーは保存します。そのときは、次式が成り立ちます。ウの場合も同様でしょう。 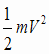 = =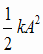 |
 |
では、一般に途中の、任意の変位x のときはどうでしょうか。その時の速度をv
とすると、運動エネルギ-はK=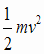 位置エネルギーはU= 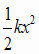 です。x=Asinωt
,v=Aωcosωt を代入すると、力学的エネルギーは です。x=Asinωt
,v=Aωcosωt を代入すると、力学的エネルギーはE = K+U = 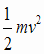 + +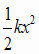 =
= 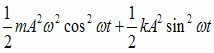 ところで、 E = 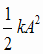 ( (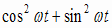 )
= )
=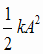 ここで、右辺ははじめの弾性エネルギーの値で一定です。
ここで、右辺ははじめの弾性エネルギーの値で一定です。というわけで、力学的エネルギー保存の法則が確かめられました。振動の間、運動エネルギーも位置エネルギーも変化しますが、合計の力学的エネルギーは一定です。 |
|
横軸に変位x、縦軸に力学的エネルギーE のグラフを作成すると、右図のようになるでしょう。E は一定で 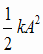 です。一方、弾性力による位置エネルギーU
はx
の二乗に比例するので、放物線を描きます。それらの差がおもりの運動エネルギーK
になっています。 です。一方、弾性力による位置エネルギーU
はx
の二乗に比例するので、放物線を描きます。それらの差がおもりの運動エネルギーK
になっています。実物の水平ばね振り子では、摩擦力や空気抵抗がいくらかあるので、エネルギー量 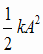 が少しずつ目減りして行くので、振幅Aがじょじょに小さくなります。その場合でも、周期は振幅Aとは無関係なので、変化しません。 が少しずつ目減りして行くので、振幅Aがじょじょに小さくなります。その場合でも、周期は振幅Aとは無関係なので、変化しません。 |
 |
減衰しない振動 減衰振動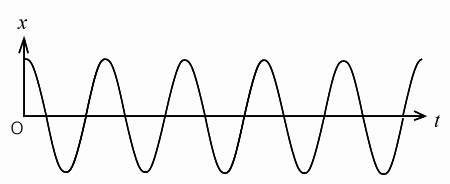
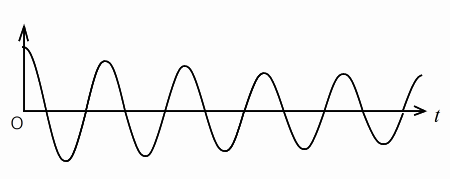
|
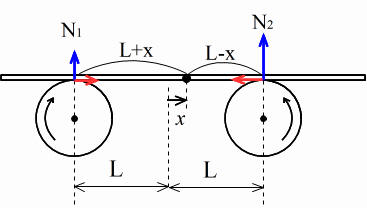
ローラー上の振動 「ばね振り子」と「単振り子」しか、教科書には出てきませんが、今回は、ちょっと変わった振動を考えます。 右図のように水平な軸で、逆向きに回転する2つのローラーがあります。その上に重さのある棒(または板)を置きます。棒は左ローラーから右向きの摩擦力を受け、右ローラーからは左向きの摩擦力を受けます。ローラーは回りつづけ、棒とローラーは常に滑っているので、棒が受ける力は、動摩擦力ですね。棒はどんな動きをするでしょうか? |
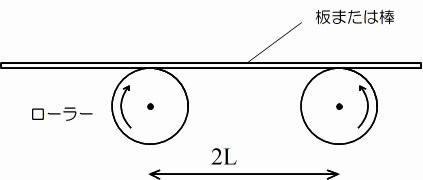 |
ヒント:①図の位置で手をはなしたら、まず、棒はどちらに動き出すでしょう。
②動摩擦力は F'=μ'N なので、垂直抗力に比例します。.
やってみました 模型モーターの軸をローラーとして、その上にまっすぐな金属棒(パイプ)を乗せました。

なぜ振動するか
上のスタート位置だと、重心が左の方にあるので、左ローラーと棒の間の押し付け合う力、つまり垂直抗力が大きいので左ローラーからの動摩擦力が勝って、右に動き出します。そして、重心が右側に移動すると、今度は右ローラーからの垂直抗力が増えるので左向きの動摩擦力が勝って、左に加速します。このように、復元力がはたらくので、質量のある棒が振動するのです。動画では単振動のように見えますが、本当に単振動でしょうか。
|
これは単振動なの? 重心の位置が中心からx右に移動している時を考えます。左右の垂直抗力をN1,N2として、それらの合計は棒の鉛直方向のつりあいから、棒にかかる重力(重さWとします)に等しく、 力のモーメントのつりあいにより、N1,N2の比はそれぞれの力の重心からの距離の逆比になるんでした。 N1 = 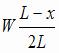 N2
=
N2
= 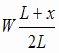 動摩擦係数をμ'、右を正方向として、棒にはたらく合力は、 F = μ'N1-μ'N2 = μ'( 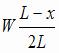 - -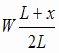 )
= - )
= -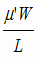 x x |
 |
復元力が変位xに比例していると計算できました。ということは,やはり,単振動なのです。
もちろん、棒とローラーの力学的エネルギーは保存しません。摩擦力もあるし、電気のエネルギーが外部から入って来ます。つまり、単振動=力学的エネルギー保存というわけではないのです。エネルギー保存、非保存にかかわらず、物体に変位に比例する復元力がはたらくなら、物体は単振動をするのです。そして、ばねの弾性力や重力など保存力だけがはたらく場合には力学的エネルギー保存の法則が成り立ちます。
練習問題1 なめらかな水平面上で,ばねの一端を壁に固定し,他端に質量0.20kgの物体をつけて単振動をさせた。その振幅は4.0cm,周期は0.40sであった。
(1) 物体の単振動のエネルギーは何Jか。
(2) 振幅を2倍にすると,単振動のエネルギーは何倍になるか。
答え:(1) 3.9×10-2J (2) 4倍
練習問題2 上のローラー上の棒の振動で、振動の周期を棒の質量mとμ',L,Wを含む式で求めよ
練習問題3
ある長さの糸の先におもりをつけた振り子がある。これを,等加速度直線運動をしている乗り物の中で,天井から静かにつるしたところ,糸と鉛直線とのなす角は45°を保っていた。この振り子を小さな角度で振らせたときの周期は,乗り物が静止しているときの周期の何倍になるか。
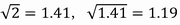 として,有効数字2桁で求めよ。
として,有効数字2桁で求めよ。
答え:0.84倍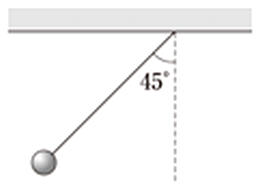
課題
☆前回の練習問題の答え合わせを十分にして、理解する。
☆今回の内容をノートにまとめる。
☆今回の練習問題 を解答する。
・完了したら、掲示板に報告しなさい。
例えば 「第**回終了」 などと報告。