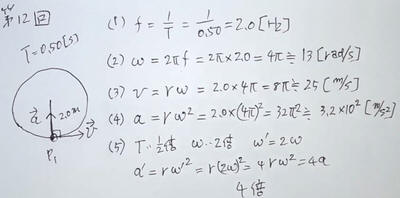
第13回 3月24日(火)
前回(第12回)の練習問題の解答動画
| → 解答 |  |
| 今回は等速円運動にはたらく力 |
|
向心力 前回、円運動している物体の加速度は中心方向だということをやりました。そうすると、運動の法則より、力が加速度の原因なので、物体にはたらく合力の方向は加速度の方向、すなわち中心方向であるということになります。たしかに、糸につながれた重りが円運動しているときは、糸が重りを引っ張っているが、もし糸が切れたら、重りはただちに円運動を終えて、等速直線運動をします。これは、ロートの実験で確かめました。円運動をさせるこの力を向心力といいます。 力の大きさは運動方程式 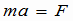 で求まるんでした。加速度の大きさは前回に で求まるんでした。加速度の大きさは前回に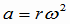 とわかっているので、円運動の向心力は次式で表せます。 とわかっているので、円運動の向心力は次式で表せます。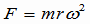 また、v=rω の関係を使って、速さv が入った形に変形できます。 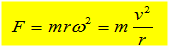 (1) (1)等速円運動では加速度の大きさは一定なので、等速円運動では向心力の大きさは一定です。方向は常に変化していますが、常に中心方向に向いています。 逆に言えば、ある一点に向かって常に一定の力がはたらくようにすれば、物体はその点を中心とする円周にそって等速円運動を続けます。 |
|
|
問い 円軌道の道路を一定の速さで進む自動車の運動では,どのような力が向心力になっているか。 答え:路面からタイヤが受ける摩擦力 必ずしも1周回らなくても、カーブは円の一部なので、カーブにそって走る車は向心力を得ているわけです。路面からタイヤが受ける力、つまり摩擦力が向心力になっています。向心力の向きはそのカーブの円の中心に向かっています。そして、向心力の大きさは、 もちろん 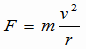 です。小回りのカーブの方が、また、速さが大きい方が大きな向心力が必要です。 です。小回りのカーブの方が、また、速さが大きい方が大きな向心力が必要です。もし摩擦力が小さく路面から向心力が十分に得られないと、車は進路をはみ出してしまいます。凍った路面などで向心力がほぼゼロになったならば、恐ろしいことに車はほぼ等速直線運動をするしかありません。 |
 |
|
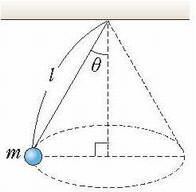
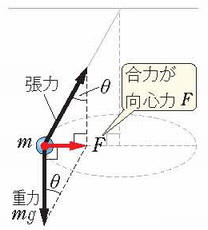
例題:円錐振り子(えんすいふりこ) 右図のように、長さ 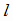 [m]の糸に質量m[kg]の重りをつるし、水平面内で等速円運動をさせる。 [m]の糸に質量m[kg]の重りをつるし、水平面内で等速円運動をさせる。(1)向心力の大きさを求めよ。 (2)周期T[s]を求めよ。 解答&解説 (1) これを「円錐振り子」といいます。「振り子」と名前が付いていますが、ぶらぶらと往復運動をするのではなく、図の角度θが一定のまま、円錐の底辺上を一定の速さでまわるのです。この運動はもちろん重力の元で起こります。重りには重力と糸の張力がかかっています。その2つの力の合力(右図の赤色の矢印)が向心力になっているのです。 図から、次の関係が成り立ちますね。 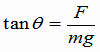 よって よって 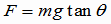 答え mgtanθ [N} (2)等速円運動の半径をr,角速度をωとすると、運動方程式ma=Fは 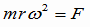 ここで r= 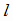 sinθ 、Fに(1)の結果を代入すれば sinθ 、Fに(1)の結果を代入すれば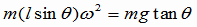 よって 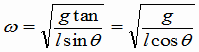 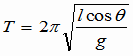 答え 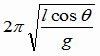 [s] [s] |
  |
|
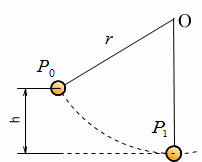
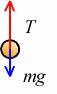
例題 質量mの重りが点Oから長さr の糸で吊り下げられいる。図のように高さhの点P0から重りを静かにはなしたら、重りは点Oの真下の点P1に達した。重力加速度をg とし, 空気抵抗は無視できるものとする。 (1)P1に達した時の速さを求めよ。 (2)P1に達した時の糸の張力を求めよ。 |
 |
|
(1)の解答 P1での速さをvとして、P0とP1の時を比較してエネルギー保存の法則から 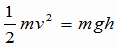 これより これより 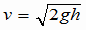 (1) (1)答え 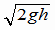 |
|
(2)の解説・解答 糸の張力をTとする。重りがP1を通る時、重りには上向きに糸の張力T、下向きに重力mgがかかっていて、それらの合力が向心力となっている。このときの運動方程式(ma=F)をたてると、加速度は 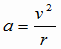 なので, なので,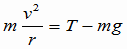 これより 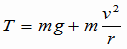 (1)式より 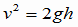 なので、上の式に代入すれば, なので、上の式に代入すれば,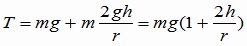 答え 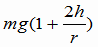 |
 |
課題
☆以上をノートにまとめなさい。
☆次の練習問題 を解答しなさい。
|
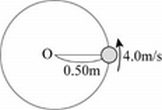
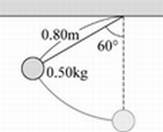
練習問題 (1) 小球の加速度の大きさは何m/s2か。 (2) 小球にはたらく向心力の大きさは何Nか。 答え (1) 32m/s2 (2) 64N 3 図のように,長さ0.80mの糸の一端に質量0.50kgの小球をつけ,他端を天井に固定する。糸がたるまないように,糸と鉛直方向とのなす角を60°にして,静かに手をはなした。重力加速度の大きさを9.8m/s2とする。 (1) 小球が最下点を通過するときの速さは何m/sか。 (2) 小球が最下点を通過するとき,糸の張力の大きさは何Nか。 答え (1) 2.8m/s (2) 9.8N |
  |
4 図のように、質量500kgの自動車が水平面を慣性で進んでいたが、その後、完全な円形のループ走路を進み、ループにそって最高点を速さ10m/sで通過し、最低点でループを抜けた。ループ内では自動車の重心が半径5.0mの円を描いていた。自動車は推進力もなく、ブレーキもかけていないとする。重力加速度をg=9.8[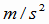 }とする。
}とする。
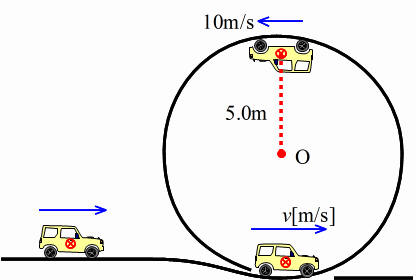
(1)水平面を進んでいた時、床から受ける垂直抗力N0はいくらか。
(2)最高点を通過する時の自動車について、運動方程式を立て、自動車がループの床から受ける垂直抗力N1の大きさを求めよ。
(3)(2)と同様にループの最低点を走る時の垂直抗力N2の大きさを求めよ。
答え:(1)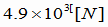 (2)
(2)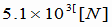 (3)
(3)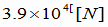
・完了したら、掲示板に報告しなさい。
例えば 「第**回 問題**まで終了」 などと報告。